 Horizontes. Revista de Investigación en Ciencias
de la Educación
Horizontes. Revista de Investigación en Ciencias
de la Educación
Https://doi.org/10.33996/revistahorizontes.v5i17.169
Enero – marzo 2021
Volumen 5 / No. 17
ISSN: 2616 - 7964
ISSN-L: 2616 - 7964
pp. 230 - 251
www.revistahorizontes.org

La resolución
de problemas y el desarrollo del pensamiento matemático
Problem
solving and the development of mathematical thinking
Resolução de
problemas e desenvolvimento do pensamento matemático
Wilver Vargas
Rojas
wilvervargas11@gmail.com
ORCID: 0000-0001-9177-0032
Universidad Autónoma del
Beni-ALSIE consultores, Bolivia
Recibido 20 de enero 2021 |
Arbitrado y aceptado 05 de marzo 2021 | Publicado en marzo 2021
RESUMEN
La resolución de problemas y el desarrollo del
pensamiento lógico erróneamente son concebidos y abordados de manera causal.
Siendo que al caracterizar la enseñanza aprendizaje de la Matemática en una
institución escolar se evidencia que los estudiantes no resuelven problemas
lógico matemático. Frente a ello, se propone una metodología de enseñanza
aprendizaje de la Matemática orientada al desarrollo del pensamiento lógico
matemático. La investigación se valió de la observación científica, el
procesamiento dialéctico y el deductivo de la información, para finalmente
arribar a una propuesta centrada en el aprendizaje desarrollador y sus
dimensiones activación – regulación, significatividad y motivación,
conjuncionado con las seis etapas o momentos de la función instructiva del
proceso de enseñanza aprendizaje que son la esencia de la propuesta
metodológica, integrando de esta manera la instrucción y el desarrollo del
pensamiento lógico Matemático.
Palabras clave: Pensamiento
lógico; resolución de problemas
ABSTRACT
Problem solving and the development of logical thinking are erroneously
conceived and approached causally. Being that when characterizing the teaching
learning of Mathematics in a school institution, it is evident that students do
not solve mathematical logical problems. Faced with this, a teaching-learning
methodology of Mathematics is proposed aimed at the development of mathematical
logical thinking. The research made use of scientific observation, dialectical
and deductive processing of information, to finally arrive at a proposal
focused on developer learning and its activation - regulation, significance and
motivation dimensions, combined with the six stages or moments of the
instructive function of the teaching-learning process that are the essence of
the methodological proposal, thus integrating instruction and the development
of logical mathematical thinking.
Key
words: Logical thinking; problem resolution
RESUMO
A resolução de problemas e o desenvolvimento do
pensamento lógico são erroneamente concebidos e abordados causalmente. Sendo
que ao caracterizar o ensino-aprendizagem de Matemática em uma instituição
escolar, fica evidente que os alunos não resolvem problemas matemáticos
lógicos. Diante disso, é proposta uma metodologia de ensino-aprendizagem da
Matemática voltada para o desenvolvimento do pensamento lógico matemático. A
pesquisa valeu-se da observação científica, do processamento dialético e
dedutivo da informação, para finalmente chegar a uma proposta voltada para a
aprendizagem do desenvolvedor e sua ativação - dimensões regulação,
significância e motivação, combinadas com as seis etapas ou momentos da função
instrutiva do ensino -processos de aprendizagem que são a essência da proposta
metodológica, integrando assim o ensino e o desenvolvimento do pensamento
lógico-matemático.
Palavras-chave:
Pensamento lógico; resolução de problemas
INTRODUCCIÓN
La resolución de problemas es una situación de aprendizaje
que ha sido adoptado casi de manera generalizada a partir de autores como
Borasi (1986), “desde el punto de vista epistemológico el problema es la
situación que muestra un determinado objeto, que genera en un sujeto la
necesidad de su modificación” (Álvarez, 2004, p. 46). Consiste en presentar
situaciones problematizadas donde existe un grado de dificultad para
resolverlos, eso determina si se trata de un problema o un ejercicio, ya que el
problema no tiene, a primera vista para el sujeto, una resolución asequible.
Diferentes investigadores han resaltado
el papel de la resolución de problemas en el proceso de enseñanza aprendizaje
de la Matemática. Entre los estudios más sobresalientes se tiene los trabajos
de Polya en Hungría y Estados Unidos (desarrolló el método denominado el
“Método de Polya” para resolver problemas de manera sistemática), Miguel de
Guzmán en España (propone una serie de métodos deductivos e inductivos para
resolver problemas), Santos Trigo en México (estudia la resolución de problemas
y plantea que se trata de una actividad esencial de aprendizaje), Schoenfeld de
la Universidad de Berkeley en Estados Unidos (investiga la resolución de
problemas llegando a caracterizar los diferentes procesos que se desarrollan
bajo este denominativo), Llivina y Jiménez (plantean un
enfoque orientado hacia el proceso de enseñanza-aprendizaje de la resolución de
problemas matemáticos),
Castellanos (desarrolla el concepto de enseñanza desarrolladora y sus
dimensiones: activación-regulación, significatividad y motivación) y Ron
Galindo en Cuba (desarrolla una estrategia metodológica a partir de las
dimensiones propuestos por Castellanos)..
En el contexto boliviano, la resolución
de problemas ha sido adoptado como elemento metodológico para la enseñanza de
la Matemática, de manera oficial, a partir de la promulgación de la Ley 1565
“Reforma Educativa” del 7 de julio de 1994, posteriormente la Ley 070 “Avelino
Siñani Elizardo Pérez” de 20 de diciembre de 2010. Sin embargo, la resolución
de problemas es implementada a partir de la tendencia curricular conocida como
la matemática moderna “cuyas bases filosóficas de este movimiento se
establecieron durante el seminario de Royamoundt, celebrado en 1959” (Álvarez,
2004, p. 45). Empero, investigadores como Capote en Pinar del Río Cuba, Ron en
Cuba, Llivina en Cuba y Vargas en Mizque Bolivia puntualizan la persistencia de
problemas en la enseñanza aprendizaje de la Matemática.
Capote (2003) sostiene que existen dificultades
en la comprensión de los problemas que no permiten una adecuada búsqueda en la
vía para la resolución, por su parte, Ron (2007) caracteriza el proceso
enseñanza – aprendizaje ineficaz en la enseñanza de la resolución de problemas,
mientras que Llivina (1999) concluye que el proceso de enseñanza – aprendizaje
es imperfecto a la hora de enseñar resolver problemas ya que se presentan
bloqueos en el proceso de búsqueda de la vía de solución. En esta línea,
también se advierte que el proceso de enseñanza
aprendizaje de la Matemática no contempla la generación de un clima afectivo y
emocional favorable para el aprendizaje, además, los momentos metodológicos:
práctica, teoría, valoración y producción, correspondientes al MESCP y la Ley
de Educación 070, se implementan sesgando el enfoque constructivista con la
búsqueda de patrones que lleve a resolver problemas implementado operaciones de
manera mecánica (Vargas, 2020).
Los
problemas que se mencionan tienen raíces metodológicas, como factor común, ya
que el proceso de enseñanza aprendizaje de la Matemática históricamente se ha
caracterizado por tener un carácter mecánico de aplicación de fórmulas y
procedimientos inalterables, hecho que no ha fortalecido la actividad mental y
los procesos de pensamiento lógico, ello justifica la necesidad de indagar
acerca de un procedimiento metodológico desarrollador de la resolución de
problemas que permita romper los esquemas tradicionales en la enseñanza y
aprendizaje de la Matemática.
Por
esta razón, el presente estudio tiene como objetivo proponer una metodología de
enseñanza aprendizaje de la Matemática orientada al desarrollo del pensamiento
lógico matemático a partir de las dimensiones del aprendizaje desarrollador:
activación-regulación, significatividad y motivación. La misma está dirigida a
los maestros del área de Matemática del nivel secundario de las unidades
educativas del subsistema de educación regular del Estado Plurinacional de
Bolivia.
Para
ello, previamente es necesario puntualizar qué es el pensamiento lógico
matemático y cual sus antecedentes. Hegel, en su Enciclopedia de las
Ciencias Filosóficas (1830) ofrece la siguiente definición “La lógica es la
ciencia de la idea pura; esto es, de la idea en el elemento abstracto del
pensamiento. […] su contenido no es otra cosa que nuestro pensamiento y sus
ordinarias determinaciones” (Hegel, 1830, p. 87).
Por
su parte, Spinoza, en su Tratado de la reforma del entendimiento (1988)
el pensamiento lógico presenta propiedades esenciales de inteligencia o
entendimiento donde sobresalen la certeza y la formalidad. Entre las
características resalta el hecho de que percibe algunas cosas o forma ciertas
ideas por sí mismo, y algunas a partir de otras; en cambio, las ideas del
movimiento, no las forma, sino atendiendo a la idea de cantidad. De la misma
manera, las ideas que forma expresan la infinitud y, las determinadas las forma
a partir de otras. O simplemente, percibe las cosas, no en una acepción finita,
si no bajo la noción de infinitud. Y, cuando imagina las cosas, las percibe en
un número fijo y con determinada duración y cantidad. Así mismo, las ideas
parecen derivarse de la sola necesidad de la naturaleza y poder humana,
mientras que las ideas confusas se forman contra la voluntad. Las ideas que
forman el entendimiento a partir de otras, la mente las puede determinar de
muchas formas por ejemplo a través de la representación, las ideas son más
perfectas cuando más perfección expresan de un objeto (Spinoza, 1988).
La
cuestión de las relaciones entre la Lógica formal y los procesos de pensamiento
atraviesa un momento de amplio debate en los medios científicos y filosóficos a
partir de la segunda mitad del siglo XIX. En estos años comienza a configurarse
la Psicología como ciencia empírica y experimental, mientras que, por otro
lado, se producen notables desarrollos en la Lógica simbólica, empezando a ser
considerada por algunos de sus cultivadores como una disciplina puramente
deductiva y formal y tratando de eliminar (en ciertos casos) cualquier alusión
a los procesos psicológicos reales de pensamiento. A partir de este momento
podrán distinguirse, a grandes rasgos, dos posturas teóricas principales en lo
referente a esta cuestión: la concepción psicologista y la logicista o
platónica.
Para
los que estudian la lógica desde una concepción psicologista, es coherente
pensar que, efectivamente, las estructuras lógicas y matemáticas son
asombrosamente exactas y objetivas, al margen del punto de vista subjetivo de
quien las considere. No obstante, si estas entidades no se corresponden con
ninguna propiedad perceptiva o física de los objetos, ni con ninguna
construcción mental o representacional; en sus escritos sobre Filosofía de la
Lógica, concretamente en El pensamiento: Una investigación lógica, Frege
(1918) sostiene que: “El pensamiento no pertenece ni a mi mundo interior como
representación, ni tampoco al mundo exterior, al mundo de las cosas
perceptibles por los sentidos” (Frege, 1918, p. 221).
La
llegada del siglo XX coincide con una nueva expansión y desarrollo de las
investigaciones en Lógica y en Psicología experimental. Diversos lógicos de
renombre optaron por la separación tajante entre las investigaciones lógicas y
las psicológicas, siguiendo la línea de pensamiento de Frege. En este sentido,
Russell (1904) opina que: “En cualquier parte de la Lógica y de las Matemáticas
la existencia de la mente humana u otra es totalmente irrelevante; los procesos
mentales son estudiados mediante la Lógica, pero el objeto de la Lógica no
presupone procesos mentales” (Henle, 1962, p. 98).
En
el siglo XX ha habido intentos de superar la dicotomía entre la postura
psicologista (Boole) y la postura logicista (Frege o Husserl). Una de las
principales aportaciones en esta línea la constituyen los trabajos de Piaget,
que han tratado de establecer una Psicología y una Epistemología genéticas de
corte naturalista y constructivista, en la que la actividad del sujeto
desempeña un importante papel en los procesos de construcción del conocimiento
científico y lógico - matemático. En los trabajos epistemológicos de Piaget
(1970) hay numerosas menciones a la posición de la Lógica en el sistema general
de las ciencias, e indicaciones de cómo surgen y se desarrollan en el curso
evolutivo (filogenético y ontogenético) del sujeto que conoce.
Piaget
(1969) considera que la Lógica y Psicología del pensamiento deben mantenerse
separados en principio, pues la Lógica formal constituiría una
axiomatización (o reconstrucción ideal) de los niveles más elevados a los que
pueden llegar los procesos intelectuales, mientras que la Psicología del
pensamiento sería una ciencia empírica que investiga cómo se piensa de hecho.
Empero, Piaget (1969) establece que pueden existir conexiones entre las dos
disciplinas, especialmente en el caso de los sujetos que disponen de la
estructura de pensamiento conocida como operacional formal.
A partir de la teoría de Piaget se
plantea como uno de los objetivos de la Matemática desarrollar el pensamiento
lógico matemático, ya que se trata del área de conocimiento directamente
relacionada con ella. Por esta razón, en los últimos años, diferentes
investigadores, han coincidido que existe una necesidad imperante de estudiar
el proceso de enseñanza aprendizaje de las Matemática debido a su impacto e
importancia en el desarrollo del pensamiento lógico (Álvarez, 2004).
El proceso de enseñanza aprendizaje, a
lo largo de la historia, ha sido parte implícita de las corrientes pedagógicas
como el humanismo, cognitivismo (constructivismo y cognitivismo) que han tenido
vigencia plena en momentos históricos, para luego ingresar a la decadencia y
dar paso a otros que guardaban mayor relación con el momento histórico y
cultural que se vivía (Álvarez, 2014).
El proceso de enseñanza aprendizaje de la Matemática ha
incorporado metodológicamente la resolución de problemas como un elemento
central en su desarrollo. Llivina
(1999) caracteriza la resolución de problemas matemáticos como
una capacidad específica que se desarrolla a través del proceso de enseñanza
aprendizaje de la Matemática. Por su lado,
Ron (2007) analiza el proceso de enseñanza
aprendizaje de la resolución de problemas, desde el proceso de enseñanza
aprendizaje desarrollador.
En este sentido la enseñanza aprendizaje desarrollador
constituye una metodología que desarrolla el pensamiento en su concepción
holística y holográfica (compleja). Castellanos (2001) define la enseñanza
desarrolladora como el “Proceso sistémico de transmisión de la cultura en la
institución escolar en función del encargo social, se organiza a partir de los
niveles de desarrollo actual y potencial de los estudiantes y conduce el
tránsito a niveles superiores de desarrollo” (Castellanos, 2001, p. 134). Estas
dimensiones son activación-regulación, significatividad y motivación.
La dimensión activación – regulación
está referida a la actividad intelectual
productiva creadora, es decir, no solo se trata de consumir y acumular información
sino buscarla y producirla, problematizarla y usarla de manera consiente. Por
su parte, la significatividad hace
referencia a las relaciones significativas en
el aprendizaje, en el área conceptual, experiencial y afectiva, es decir, la
formación de sentimientos, actitudes y valores que son fundamentales en el
siglo XXI. Y la motivación
trabaja lo relacionado con las motivaciones
intrínsecas hacia el aprendizaje, es decir, al sistema de autovaloraciones y
expectativas positivas con respecto al aprendizaje.
En este sentido, la implementación de
diferentes técnicas y estrategias en base a las dimensiones
activación-regulación, significatividad y motivación hace posible desarrollar
el pensamiento lógico matemático.
MÉTODO
El estudio se lleva adelante implementando el método
empírico de la observación científica que
permitió indagar acerca de las funciones del proceso de enseñanza aprendizaje a
partir de sus componentes internos (problema, objeto, objetivo, contenido,
método, medio, forma, resultado y evaluación) adoptado de Álvarez (2004).
Trabajando de esta manera con docentes y estudiantes de segundo curso del nivel
secundario constituyendo un estudio censal.
La dimensión teórica se trabaja con el
método dialéctico y el método el hipotético deductivo. La dialéctica es
adoptada como corriente teórica fundamental, permitió analizar a partir de la
identificación de elementos y componentes que surgieron de estudios precedentes
(contradicción, complementación y mutua necesidad). El método hipotético
deductivo constituye una forma de abordaje transversal del tema de estudio,
haciendo posible arribar a algunas conclusiones surgidas de una hipótesis, es
decir, las mismas se alcanzan deductivamente.
La metodología que se elaboró para
realizar la propuesta contempla el abordaje de la dimensión significatividad
presente a la hora de resolver problemas matemáticos desde los procesos
psíquicos que intervienen en el proceso de resolución de los problemas, por ser
esta una actividad intelectual, “los procesos que intervienen en ella son
predominantemente cognitivos” (Llivina, 1999, p. 52), complementados por la
dimensión motivación que representa la intervención de procesos
emocionales y volitivos constituyendo de esta manera “el pensamiento mismo,
como proceso psíquico real, una unidad de lo intelectual y lo emocional”
(Rubinstein, 1965, p. 208).
La dimensión activación – regulación contempla
las capacidades intelectuales: memoria, imaginación, pensamiento y senso -
percepción están presentes en la resolución de problemas, haciendo referencia a
las operaciones a través de las cuales el sujeto desarrolla la actividad
intelectual (Rubinstein, 1995). La activación- regulación
“expresa la caracterización cualitativa de las acciones intelectuales, por
ende, de los procesos sobre cuya base transcurren” (Llivina, 1999, p. 54)
Las
dimensiones dan pie a las seis etapas metodológicas cuyo mayor aporte es la
integración de las acciones para resolver problemas y un proceso eslabonado de
tareas. Han sido diseñados sobre la base las seis atapas de la función
instructiva de la Teoría de los Procesos Consientes de Álvarez (2014).
1. Primera etapa: Motivación y sentido
La
“motivación” en términos pedagógicos está relacionado con mostrar al estudiante
aquello que no conoce y que se le quiere enseñar y al mismo tiempo hacerle
entender que tiene la necesidad de aprender porque es muy importante. Está
directamente relacionada con la primera acción para resolver problemas que se
refiere a comprender el problema, para ello el sujeto tendrá que analizar, a
partir de la lectura detallada del problema, separando lo dado de lo buscado,
para lograr hallar alguna palabra clave u otro recurso que permita encontrar
una adecuada orientación en el contexto de actuación.
Relacionar los elementos previamente analizados para expresar el
problema con sus palabras o con un sistema simbólico abreviado o realizando una
figura de análisis, construyendo una tabla o elaborando cualquier medio que
sirva para modelar el texto. Para la realización de esta acción el
sujeto deberá ejecutar operaciones propias del contexto matemático en el que
está enunciado el problema.
2. Segunda etapa o momento: Información del contenido en
lenguaje lógico
Se
trata de un momento donde el docente explica a partir de un mapa de contenido
el objeto o contenido, los conceptos, categorías, propiedades, magnitudes,
clasificaciones, métodos de resolución de operaciones, resolución de casos de
factorización, etc., de manera gráfica y sencilla, empleando un lenguaje
apropiado.
Es
un momento que vincula al estudiante con los conocimientos que le permitirán no
solo resolver problemas de naturaleza didáctica, sino responder con
herramientas científicas a algunos problemas de su comunidad o familia. Para
una explicación más precisa, Condemarín (1996) propone:
La
expresión verbal de un juicio lógico: negación, conjunción, disyunción y uso
de cuantificadores, así mismo, la expresión simbólica de un juicio lógico:
falso o verdadero, negación, conjunción y disyunción, así mismo, la noción
de conservación: conservación de longitud, conservación de cantidad
discontinua, conservación de cantidad continua, conservación de peso,
conservación de número, Conservaciones de la equivalencia de dos conjuntos en
correspondencia, Conservación de superficie, también la noción de seriación:
seriación simple, seriación múltiple y la noción de clase: clasificación según una
propiedad, clasificación simple y Noción de inclusión (Condemarín, 1996, p.
360-361).
3. Tercera etapa o momento: La asimilación del contenido
Es
el momento de resolver problemas, inicialmente por parte del docente para que
posteriormente también lo realicen los estudiantes sin perder de vista aquello
que se había socializado en la etapa anterior ya que muchas de las
interrogantes permitirán complementar el aprendizaje de los estudiantes.
Los
procesos para resolver problemas puede comprender métodos como los propuestos
por Polya en Álvarez (2004): que contempla comprender el problema, concebir un
plan, ejecutar el plan y examinar la solución obtenida. Así mismo, el
matemático Miguel de Guzmán plantea algunos métodos para la resolución de
problemas, como la Resolución gráfica y Ensayo-error: cuyos pasos
son: 1. Escoger una posible solución, 2. Efectuar las opresiones planteadas y
probar si satisface al problema, 3. Se reajusta los procedimientos y se aplican
las nuevas posibles soluciones hasta llegar a satisfacer el problema.
4. Cuarta etapa o momento: La producción;
puesta en práctica del contenido
Se trata de una etapa o momento que presta atención a las
inquietudes de los estudiantes que estén relacionadas con las actividades
productivas y económicas propias de las familias y la comunidad. Presta
atención a las cifras y los problemas de manera pormenorizada y a los métodos
que se aplican.
El
sujeto deberá ejecutar las operaciones de sintetizar al unificar los
elementos separados en el análisis del problema para poder escribir la solución
del mismo, considerando sólo aquellas propiedades que son necesarias o
suficientes para la solución y aplicar, utilizando los elementos obtenidos en
el análisis del problema en la solución del mismo.
5. Quinta etapa o momento: La sistematización del nuevo
contenido
Constituye una etapa de
organización a nivel de esquemas mentales los conocimientos nuevos a los ya
existentes. Para ello será necesario relacionar
elementos y componentes que surgieron en el proceso de resolución de problema, analizar
el procedimiento implementado y sintetizar cada los procesos a partir de los
elementos, componentes y algoritmos aplicados.
6. Sexta etapa o momento: Evaluación del aprendizaje
La evaluación es
fundamental para el proceso, es así que se puede aplicar los diferentes tipos
de evaluación. a) Según su finalidad y función: formativa y sumativa; b)
según su extensión: global y parcial; c) según los agentes:
interna (autoevaluación, heteroevaluación y coevaluación) y externa (evaluación
de expertos); d) según el momento de aplicación: inicial, procesual y
final. Se considera necesario enfocar el interés de la evaluación en el logro
del objetivo, en la medida que se tenía planificado, debido a que la prioridad
en la asimilación y acomodación o internalización de nuevos aprendizajes.
RESULTADOS
Como se puede advertir
el desarrollo del pensamiento lógico matemático no solo ha dejado de ser una
prioridad sino que la misma no es trabajada desde los primero cursos en las
Unidades Educativas del Sistema Educativo Plurinacional.
Capacidades y habilidades lógicas
según Piaget
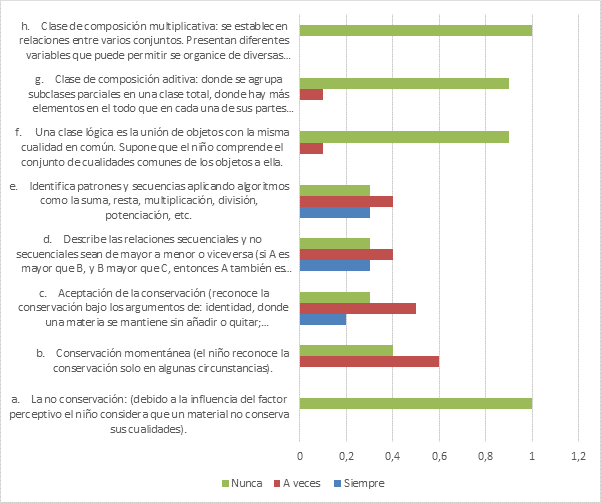
Nota:
Para el cálculo de los porcentajes se utilizó una tabla de frecuencias
Las nociones no solo
constituyen razonamientos fundamentales que
están relacionadas con una determinada edad o periodo operatorio, en la
Matemática es recurrentes su aplicación por ser parte constitutiva de un
razonamiento para desarrollar un contenido. La no conservación (debido a
la influencia del factor perceptivo el niño considera que un material no
conserva sus cualidades). De todas las clases observadas el 100% de las veces
no se emplea este razonamiento, peor aún de manera planificada.
La
Conservación momentánea (el niño reconoce la conservación solo en
algunas circunstancias). Al respecto se observa que el 60% de las veces, a
veces se utiliza este razonamiento, sobre todo en algunas explicaciones del
maestro, mientras que el 40% de las veces no se emplea aquello.
La
aceptación de la conservación (reconoce la conservación bajo los
argumentos de: identidad, donde una materia se mantiene sin añadir o quitar;
reversibilidad, una materia retoma su estado inicial a pesar de haber sido
modificada de forma). Los resultados revelan que el 20% de las veces se emplea
este razonamiento, así mismo, el 50% de las veces solo aparece esporádicamente
y el 30% de las oportunidades no se lo emplea.
La
“noción de seriación” que se hace evidente en las habilidades lógicas como:
Describe las relaciones secuenciales y no secuenciales sean de mayor a menor o
viceversa (si A es mayor que B, y B mayor que C, entonces A también es mayor
que C.). La habilidad es trabajada en un 30% de manera frecuente, es decir,
siempre está presente, un 40% de las veces solo se presenta a veces y los otros 30% de las
oportunidades no se hace referencia alguna. En lo que respecta a la
identificación de patrones y secuencias aplicando algoritmos como la suma,
resta, multiplicación, división, potenciación, etc., se aprecia que 30% de las
veces se trabaja este razonamiento, pero el 40% de las oportunidades solo a
veces y los otros 30% restantes no se advierte el uso y manejo del
razonamiento.
La “noción de clase” es
la tercera de las nociones que por alguna razón es la menos trabajada una
clase lógica es la unión de objetos con la misma cualidad en común. Supone
que el niño comprende el conjunto de cualidades comunes de los objetos a ella.
Esta habilidad es trabajada el 10% de las veces esporádicamente, y el 90% de
las veces no ocurre aquello. Otro razonamiento de clase es la denominada clase
de composición aditiva: donde se agrupa subclases parciales en una clase
total, donde hay más elementos en el todo que en cada una de sus partes (A+B=C,
donde A es mayor que B). Este razonamiento se evidenció el 10% de las veces de
manera esporádica y, los restantes 90% de las oportunidades no se trabaja dicha
habilidad. Una tercera habilidad es la referida a la clase de composición
multiplicativa: es aquella que busca se establezcan relaciones entre
varios conjuntos. Presentan diferentes variables que puede permitir se organice
de diversas formas.
El desarrollo de las
capacidades y habilidades lógico matemáticos está relacionado con el logro de
procesos lógicos, los mismos constituyen un elemento central del análisis de
los procesos ejecutados. Al respecto se tiene los siguientes resultados.
Procesos
lógicos relacionados con la matemática según Álvarez de Zayas

Nota:
Para el cálculo de los porcentajes se utilizó una tabla de frecuencias
Se
observa que los procesos lógicos que se desarrollan en la enseñanza-aprendizaje
la Matemática son reducidos, como se advierte: El Análisis que expresa
la descomposición del objeto de estudio en sus partes, sobre el mismo, según lo
observado se advierte: siempre el 0%, a veces 50% y nunca 50%.
Sintetizar: expresa la
integración de las partes constitutivas. Se advierte: siempre 0%, a veces 0% y
nunca el 100%.
Inducir: expresa la
influencia de lo particular a lo general. Al respecto: siempre 20%, a veces
50%, nunca 30%.
Deducir: expresa la
influencia de lo general a lo particular. Se evidencia que: siempre 0%, a veces
0% y nunca 100%.
Explicar: se
caracteriza un objeto en sus rasgos más internos y esenciales, los resultados:
siempre el 0%, a veces 30% y el 70% nunca. La explicación lo realiza el docente
abarcando aspectos procedimentales para la resolución de las operaciones.
Demostrar: se prueba con
evidencia o muestras inequívocas la verdad de una proposición, al respecto se
observó que: Siempre 80%, a veces 20%, nunca 0%. La demostración es parte
esencial de la enseñanza de la matemática, sin embargo, al no estar planificado
este proceso se limita solo al maestro.
Razonar: se estructura
una lógica u orden de juicios encaminado a demostrar algo. Se observa:
Siempre 0%, casi siempre 0% y nunca el 100%. En el proceso de resolución de
problemas solo se aprende a resolver operaciones.
Concretar: procedimiento
mediante el cual se caracteriza el objeto en sí mismo. Se advierte: siempre 0%,
casi siempre 0% y nunca 100%. No se aplica el proceso lógico.
Derivar: proceso
mediante el cual se infiere el origen de un objeto. El 0% siempre, 40% a veces
y el 60% nunca. Se evidencia que se emplea al derivar algunas operaciones de
otras.
Relacionar: se establecen
los nexos entre los componentes de un objeto o entre objetos. Se observa:
siempre 0%, casi siempre 0% y nunca el 100%. No se alcanza procesos de este
nivel.
Determinar: proceso en el
cual se precisa un objeto de estudio. Al respecto se observa: 0% siempre, 0%
casi siempre y 100% nunca, ya sea de manera práctica o teórica.
Identificar: se precisan
las características iguales de dos o más objetos de estudio. Al respecto:
siempre 0%, casi siempre 20% y 80% nunca. Se lo emplea para reconocer el tipo
de operación Matemática.
Igualar: proceso
mediante el cual se precisan las características iguales de dos o más objetos
de estudio. Se observó su implementación con los siguientes resultados: siempre
0%, casi siempre 30%, y nunca 70%. Se lo emplea como parte del lenguaje
matemático sin hacer referencia directa a procesos lógicos.
Integrar:
proceso de composición del objeto, de sus partes y sus características.
Los resultados reflejan una aplicabilidad: siempre 0%, casi siempre 0% y nunca
100%.
Comparar: se precisan
las características similares y diferencias entre dos objetos de estudio. Se
advierte: siempre 0%, casi siempre 0% y nunca 100%. No se emplea el proceso
lógico.
Aplicar: se hace uso
de una cierta inferencia en la práctica para transformar una situación. Al
respecto se observó: siempre 0%, casi siempre 0% y nunca 100%. Se emplea el
concepto para utilizar un algoritmo y no como proceso lógico útil en el procedimiento.
Clasificar: se agrupa un
conjunto de objetos en correspondencia con cierta característica. Se evidencia
los siguientes resultados: siempre 0%, casi siempre 50% y nunca 50%. Se lo
maneja como adjetivo para algunas tareas.
Relacionar: se establece
el vínculo entre dos o más características de un objeto de estudio o con otros.
Los resultados muestran su uso: siempre 0%, casi siempre 0% y nunca 100%. No se
emplea el proceso lógico.
Abstraer: proceso de
separar subjetivamente solo un aspecto del objeto. La aplicación de este
proceso lógico arroja lo siguiente: siempre 0%, casi siempre 0% y nunca 100%.
No se emplea el proceso lógico.
Generalizar: proceso en el
que se establece la característica común de dos o más objetos. La observación
muestra: siempre 0%, casi siempre 0% y nunca 100%, no se emplea el proceso
lógico.
Como
se puede advertir la enseñanza aprendizaje de la Matemática no está orientada
al desarrollo del pensamiento lógico matemático, por lo tanto, se plantea la
siguiente:
Propuesta
metodológica
La
misma permite concretar en tres fases las actividades que se deben llevar
adelante, involucrando las dimensiones del aprendizaje desarrollador, las
etapas o momentos metodológicos y los procesos lógicos concordantes con cada
una de ellas. Se inicia con una prueba de carácter proposicional del
diagnóstico
Fase
I: Prueba Objetiva de Diagnóstico
¡Lee con cuidado todos
los ejercicios antes de empezar a resolver!
1. Un día Juan se
encuentra ante un cierto número de objetos diversos como ser vasos de plástico,
piezas de madera, platos de porcelana, una esponja para lavar platos, cucharas
de madera, plástico y metal, un carrito de plástico y varias pelotitas de
plástico. Todas ellas son colocadas en un recipiente con agua. A partir de lo
que va ocurriendo con cada uno de las piezas debes clasificar en grupos ¿qué
grupos podría surgir y por qué?
Anota
en los recuadros los objetos que correspondan a un grupo (ponga un nombre a
cada grupo), puedes añadir más recuadros en caso de ser necesario:
2. ¿Por qué algunos objetos flotan y otros
no?
R:
____________________________________________________________________________________________________________
Resuelve las
siguientes operaciones:
3. Las
longitudes de los lados de un triángulo son 19mm, 32mm, 13mm.
Determine el perímetro del triángulo.
R:
____________________________________________________________________________________________________________
 4.
Las rectas l y m son paralelas. ¿Cuál
es la amplitud del ángulo x?
4.
Las rectas l y m son paralelas. ¿Cuál
es la amplitud del ángulo x?
 C 78°
C 78°
 I x
I x
 m B
m B
D 100 E
R: __________________________________________________________________________________________________________
5. Las longitudes
de los lados
de
un triángulo se expresan como x
+1, 7–x,
4x
– 2.
Determina todos los valores que puede tomar x para que el triángulo sea isósceles.
R: __________________________________________________________________________________________________________


 6. En la figura
MN ll PQ, RN bisectriz del ángulo SRQ y Ө = 20.
6. En la figura
MN ll PQ, RN bisectriz del ángulo SRQ y Ө = 20.
Clasifique el triángulo PQR
según la longitud de sus lados y según la amplitud.de sus ángulos.
 S
S

 M R N
M R N

 P Q
P Q
Ө
R:
__________________________________________________________________________________________________________
Los ejercicios planteados presentan los siguientes criterios:
Un ejercicio sin solución, un ejercicio con varias vías de solución
y un ejercicio que vincula la geometría con el trabajo con variables. Esto se trabajó
con la finalidad de analizar los aciertos,
los errores, pero por sobre todo la utilización de diferentes vías de solución que constituyen el reflejo de la
capacidad específica a la hora de resolver problemas.
En
este sentido, los resultados del
diagnóstico
proporcionan elementos que permiten tomar decisiones acerca de la metodología,
los contenidos, los objetivos y las metas. Dicho proceso de análisis se
lo realiza sobre la base de dimensiones e indicadores siguientes:
a. Dimensión
Motivación:
|
Indicadores
|
Muy
buena (4)
|
Buena
(3)
|
Regular (2)
|
Mala
(1)
|
|
1. Interés personal
por
aprender matemática.
|
|
|
|
|
|
2.
Interés personal por resolver problemas.
|
|
|
|
|
|
3. Presenta la seguridad necesaria para esforzarse.
|
|
|
|
|
|
4. Persevera a pesar
de los obstáculos que puedan
surgir.
|
|
|
|
|
b. Dimensión Activación- regulación
|
Indicadores
|
Muy buena
(4)
|
Buena (3)
|
Regular (2)
|
Mala (1)
|
|
1. Independencia.
|
|
|
|
|
|
2.
Originalidad.
|
|
|
|
|
|
3.
Fluidez.
|
|
|
|
|
|
4. Flexibilidad.
|
|
|
|
|
|
5. Logicidad.
|
|
|
|
|
|
6. Profundidad.
|
|
|
|
|
|
7. Organización.
|
|
|
|
|
c. Dimensión: Significatividad
|
Indicadores
|
Muy
buena (4)
|
Buena
(3)
|
Regular (2)
|
Mala (1)
|
|
1.
Significatividad conceptual.
|
|
|
|
|
|
2. Significatividad experiencial.
|
|
|
|
|
|
3. Significatividad afectiva.
|
|
|
|
|
|
4. Analiza las
consecuencias de los contenidos
|
|
|
|
|
|
5. Solidaridad.
|
|
|
|
|
|
6. Responsabilidad.
|
|
|
|
|
En los cuadros se
desglosan las dimensiones en indicadores que son calificadas con criterios: Muy
Bueno (4), Bueno (3), Regular (2), Malo (1); una vez centralizado permite
apreciar los niveles de desarrollo de las diferentes dimensiones.
Fase II de Implementación: Ejecución de las
acciones del aprendizaje desarrollador y las etapas metodológicos
Las diferentes dimensiones serán trabajadas tomando en cuenta
tres momentos: el primer momento es la explicación de las consignas de trabajo.
El segundo momento será trabajada de manera individual o grupal aplicando
métodos heurísticos y, por último, se implementará el momento de la evaluación
que servirá para analizar los aciertos y desaciertos que se hayan tenido al
momento de resolver los problemas.
Para llevar adelante la
propuesta metodológica se debe adoptar las siguientes medidas:
·
La cuidadosa preparación de los ejercicios
y problemas a utilizar en las clases; así como los métodos de enseñanza y las formas en que presentan los ejercicios y problemas.
·
La participación activa y motivada de los estudiantes.
Para
desarrollar el pensamiento lógico matemático se debe potenciar las dimensiones
del aprendizaje desarrollador como ser: a. activación – regulación, b.
significatividad, y c. Motivación. En este sentido, se presentan los problemas
adecuadas dirigida a cada una de las dimensiones, las mismas que son reforzadas
con las etapas o momentos metodológicos.
Dimensión Motivación
Se puede trabajar ejercicios y problemas donde se utilicen: cuadrados mágicos, varillas de igual longitud, soluciones novedosas,
contar, como vía de solución.
1. En un cuadrado mágico la suma de las
casillas
horizontal,
vertical
y diagonal es
siempre
la misma. En el
siguiente cuadrado
mágico
A+B+C=-34,5. Halla A, B, C,
D y
E
R: D=-6,9;
E=-16,1;
A=-2,3;
C=-20,7; B=-11,5
(Cuadrados mágicos)
2. Se pretende dividir el tronco cilíndrico de la figura en 8 trozos iguales,
pero solamente con tres
cortes. ¿Cómo serían esos cortes?

 R:
R:
 (Soluciones novedosas)
(Soluciones novedosas)
3. Diga cuántos
rectángulos
hay
en la siguiente figura.
R: 9. (Conteo, establecer un orden)
4. Si en un momento determinado adelanta usted al segundo, ¿en qué lugar
se colocaría?
R: en segundo (Búsqueda de alternativas
creativas)
Dimensión Activación-regulación
Para ejecutar las acciones orientadas a la
dimensión activación-regulación, se toman en cuenta los siguientes tipos de
ejercicios:
Ejercicios con
solución
única:
1.
Construya un rombo en el que
una
de sus diagonales sea igual a uno
de sus lados.
R: A partir de la utilización de la amplitud de los ángulos de un triángulo
equilátero, se llega a que son, 60º, 60º, 120º, 120º. (Estrategia: graficar, analizar casos particulares, establecer relaciones, buscar regularidades).
2. En una selva hay algunas hienas, águilas y serpientes. Cada mañana, cada una de las hienas se come un águila. En la tarde cada serpiente se
come
una hiena. Por la noche cada águila se come una serpiente. Al final del tercer día solo queda un águila. ¿Cuántos animales de cada tipo había al principio?
R: Hienas 13, Águilas 19, Serpientes 9 (Estrategia: trabajo hacia atrás)
Orientaciones al
profesor: promueve la utilización de estrategias generales
como:
tanteo inteligente,
hacer un diagrama,
usar las propiedades, resolver
un ejercicio equivalente,
trabajar hacia atrás, reformular
el problema, tomar un descanso y después intentarlo
y promover que se valore la utilidad de la estrategia usada, y bajo qué condiciones
se puede volver a utilizar.
 Ejercicios con
más de una solución:
Ejercicios con
más de una solución:
1. Si la siguiente pieza representa un cuarto de otra.
Representa más de tres piezas enteras con la condición de que al menos uno de sus lados
descanse sobre una línea horizontal
imaginaria.





 R:
R:




2.
Determinar operaciones combinadas de aritmética cuyo resultado
final sea 13. Incluir las 4 operaciones elementales (+, -, ·, :) al menos una vez, o alternativamente, exactamente una vez.
R: ((22+5) ·2-1):4; (Infinitas soluciones)
3. Todos
los
dígitos escondidos en la adición son impares diferentes.



 Reconstruye la adición. +
Reconstruye la adición. +
R: 19
37 17 39
+37 +19 +39 +17
56 56
56 56

 6
6
Orientaciones al profesor: Dejar que los estudiantes intenten
resolver el ejercicio sin importar la vía
que utilicen,
valorar cada una de las vías
y soluciones encontradas,
y exigir la
búsqueda de otras,
pedir la fundamentación de otras soluciones encontradas, trabajar con los datos para obtener situaciones y soluciones diferentes que incluso pueden ser hasta
únicas y sin solución.
Ejercicios sin solución:
1. ¿Cuál es
el
perímetro del
triángulo de lados 94mm, 177mm y 83mm?
R: N.S. No existe el triángulo (Datos contradictorios)
2.
¿Cuáles pueden ser las dimensiones de un cuadrado, si se sabe que la longitud de sus lados
son
cantidades enteras, su área es menor que 160
cm2 y el
número que representa su área termina en dos?
R: N.S. (ningún cuadrado perfecto termina en dos)
3. La suma de tres números pares consecutivos es 57. ¿Cuáles son esos
números?
R: N.S. (La suma de tres números pares siempre es par)
Orientaciones al profesor. Dejar que los estudiantes resuelvan el
ejercicio, sin importar que no encuentren que no tiene solución. Si el
estudiante da alguna respuesta como solución: Que explique cómo llegó a la solución,
buscar contraejemplos, y cuestionar la solución hasta que el estudiante identifique que ese ejercicio no tiene solución.
Que el estudiante explique por qué no fue capaz de llegar a que no tiene
solución.
Que el estudiante reformule el problema para que tenga solución, que
puede ser hasta más de una.
Ejercicios contra el tiempo:
1. Calcula:
a)
36 – 25 = R:11
b) (50 – 49)
+ (49 – 48)
+ (48 – 47)
+ +(2 – 1) = R:49
c) 2 – (1 – (2 – (1 – (2 – (1 – 2))))) =
R: 5
2. Ana dibuja todos los triángulos de lados enteros y perímetro 9. Patricia dibuja todos los triángulos de lados
enteros y perímetro 10. ¿Cuál
de
las dos dibuja más triángulos?
R: Ana 3, Patricia 2. Ana dibuja más triángulos.
Orientaciones al profesor: Determinar
un tiempo para
dar
la solución.
Al concluir el tiempo
discutir las vías
desarrolladas,
las soluciones encontradas,
si no se encontraron, sugerir, intercambiar, nunca resolverlo,
si se encontraron, reconocer
el trabajo desarrollado.
Dimensión Significatividad
Para
la puesta en práctica de la dimensión significatividad se plantean los
siguientes ejercicios:
Ejercicios con omisión de condiciones o
preguntas, o adición de
información no relevante para el proceso de solución:
 1. La figura ABCD es
un
rectángulo de área
24cm2. D C
1. La figura ABCD es
un
rectángulo de área
24cm2. D C
 E
es el punto medio de AB .
E
es el punto medio de AB .
¿Qué porciento representa el área sombreada A E B
del área del rectángulo?
R: 75% (Por diferencia de áreas, proporcionalidad, casos particulares)
2.
Esteban ya ganó 50 de 75 juegos contra su computadora. Si quiere sostener en
total 105 juegos. ¿Cuántos juegos más tiene que ganar para que al final de la
jornada le haya ganado a su computadora el 60% de los juegos?
R:
13 juegos
3. Si el valor de A es el 30% del de B, el
valor de B es el 40% del de C y el valor de D es
el 60% del de C. Calcula A/B
R: 3/10
Orientaciones
al profesor. No adelantar información al estudiante, dejar que éste
intente resolverlo con sus propios conocimientos. Si los estudiantes no
utilizan la información no relevante, se pedirá que justifiquen su no
utilización, y se orientará la elaboración y resolución de un nuevo problema
sin la información no relevante.
Si
los estudiantes utilizan la información no relevante, se orientará resolverlos
sin esta información y comparar las soluciones hasta que se identifique la no
necesidad de la información para el proceso de resolución. De esta manera, se
alcanzará la sistematicidad.
Fase III: Evaluación
del desarrollo de las dimensiones
El cuestionario será auto aplicado ya que se pretende
llevar adelante un proceso de autoevaluación orientada a reflexionar el proceso
y las operaciones implementado en la búsqueda de desarrollar las dimensiones
del aprendizaje desarrollador por su intermedio el pensamiento lógico
matemático. Posteriormente se sugiere evaluar los indicadores que posiblemente no
han sido lo suficientemente trabajadas.
Discusión
Para Koliaguin (1975) el pensamiento
matemático se caracteriza por la profundidad, la amplitud, el carácter
autocrítico del pensamiento y la flexibilidad. Mientras que Rodríguez (2003)
considera al pensamiento lógico matemático es una capacidad que permite
interpretar información en la vida diaria, tomar decisiones en función de esa
interpretación, usar herramientas matemáticas incluyendo la modelación, el
pensamiento analítico, crítico y flexible. Adoptando ambas definiciones se
advierte que es amplio y no se cierra a una actividad concreta, sin embargo,
sus características la hace distinta a otras habilidades del pensamiento (Spinoza, 1988).
A partir de los estudios y el método de
Polya (1973) acerca de la enseñanza de la Matemática donde los contenidos pasan
a un segundo plano frente a la prioridad de desarrollar el pensamiento lógico
matemático surgen diversas propuestas fruto de investigaciones y estudios en el
campo de la Didáctica de la Matemática, como la de Müller (1978), Schoenfeld
(1985) y Santos (1993).
Müller (1978) desarrolla lo que se
denomina instrucción heurística, que se resume en procedimientos para facilitar
la búsqueda de la vía de solución, constituyen un sistema que abarca: 1.
Orientación hacia el problema; 2. Trabajo en el problema; 3. Solución del problema
y 4. Evaluación de la solución y la vía. Por un lado, Schoenfeld
(1985), integra la resolución de problemas con el desarrollo del pensamiento
lógico matemático, y cuyo método comprende: 1. Comprensión del problema; 2.
Diseño de un plan de solución; 3. Ejecutar el plan y 4. Mirada retrospectiva. Y
por otro lado, Santos (1993) modela el proceso de resolución en ocho fases,
inspirados en el desarrollo de una investigación científica: 1. Consciencia
de la existencia del problema; 2. Supresión de los dados; 3. Interés por la
situación problemática abordada; 4. Análisis cualitativo; 5. Formulación de
hipótesis; 6. Estrategias de resolución; 7. Análisis de los resultados y 8.
Maduración.
Los métodos propuestos por Müller
(1978), Schoenfeld (1985) y Santos (1993) comprenden diferentes procesos
lógicos de carácter sistémico. Entre sus coincidencias se puede advertir que
parten de la comprensión o la conciencia de que existe un problema, para luego
plantear o buscar una solución que puede ser deducido, inferido o hipotetizado,
la resolución pasa por un momento de planificación y ejecución que será
desarrollada
a partir de los datos y los
conocimientos previos que tenga el individuo y, finalmente culminar con una
evaluación del resultado que permitirá verificar si los datos alcanzados
satisfacen al problema, en caso de no ser así, será necesario replantear y
ejecutar nuevamente el procedimiento. El proceso la resolución de problemas no
solo pasa por la ejecución de una o varias operaciones matemáticas, sino
también, el razonamiento lógico. Sin embargo, los autores no prestan mucha
atención al desarrollo sistemático de las operaciones lógicas (ej. Analizar,
deducir, caracterizar, comparar) que son fundamentales a la hora de solucionar
un problema sean cuantitativos o cualitativos (Álvarez, 2004).
De la misma forma, la resolución de
problemas a girado en torno al contenido, siendo este el componente central del
proceso de enseñanza aprendizaje de la Matemática, ya que la resolución de
problemas se utiliza como el mecanismo para enseñar un contenido, situación que
no permite desarrollar el pensamiento lógico matemático como prioridad. A pesar
que existe una estrecha relación entre la resolución de problemas y el
desarrollo del pensamiento lógico matemático, ya que se incita al
estudiante a implementar procesos característicos del pensamiento lógico
(Silvestre, 2001).
En el presente estudio, el autor pudo
advertir que los maestros sostienen y enseñan empleando la resolución de
problemas sin emplear un método concreto correspondiente a un autor, lo que ha
generado un sesgo no solo en lo metodológico sino también en el enfoque
constructivista, que aun predomina como enfoque pedagógico. Dicho sesgo se traduce
en la identificación de uno o dos operaciones matemáticas para luego aplicar
mecánicamente y arribar a la solución. Por lo tanto, no se desarrolla el
pensamiento lógico, ya que la repetición y mecanización no facilitan aquello.
Castellanos (2001) considera que el
desarrollo del pensamiento matemático no pasa solo por el trabajo sistemático
de las habilidades y capacidades directamente relacionadas a ella, a criterio
de la autora es necesario trabajar de manera integral y holística las
dimensiones activación-regulación, significatividad y motivación. Las mimas
abarcan el desarrollo no solo del pensamiento sino también del lenguaje, ya que
ambos se necesitan, complementan a pesar de ser contrarios (relación
dialéctica), los valores humanos y espirituales también son parte del
desarrollo del pensamiento lógico matemático. El autor se adscribe al
planteamiento de Castellanos (2001) comprendiendo que el pensamiento lógico
matemático involucra el desarrollo de otras habilidades y capacidades como ser
el lenguaje, los valores humanos y espirituales que en la vida cotidiana no
están desvinculados unos con otros.
A las dimensiones del aprendizaje
desarrollador se integran las fases o momentos de la función instructiva del
proceso de enseñanza aprendizaje de Álvarez (2004). Las dimensiones:
motivación, activación-regulación y significatividad guardan relación directa
con las etapas: motivación, información del contenido, asimilación del
contenido, dominio del contenido, sistematización del nuevo contenido y la evaluación
del aprendizaje (Álvarez, 2004). Dando paso a las etapas: motivación y sentido,
información del contenido en lenguaje lógico, asimilación del contenido,
producción puesta en práctica del contenido, sistematización del nuevo
contenido y, evaluación del aprendizaje.
La
relación entre las dimensiones del aprendizaje desarrollador y las etapas
metodológicas, así como su relación con los componentes del proceso de
enseñanza aprendizaje se presenta en el siguiente cuadro:
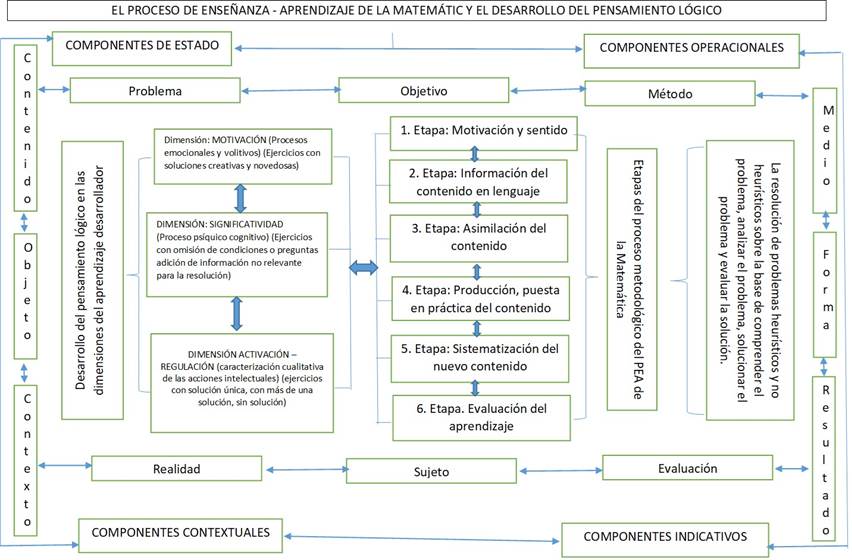
CONCLUSIONES
El estudiante no debe ser concebido como
un sujeto que sigue un conjunto de pasos para resolver problemas, sino como
aquel que moviliza y desarrolla su pensamiento matemático en la búsqueda
de vías de solución a diferentes problemas que se le presenten.
El desarrollo del pensamiento lógico
matemático es y será una de las prioridades de la educación impartida por las
Unidades Educativas del sistema regular, su alta importancia radica en que la
tecnología y su lenguaje algebraico, el sistema binario y otros contenidos y la
habilidad de manejarlo de manera creativa es y será aún más fundamental con el
mayor avance de la ciencia y la tecnología.
La propuesta metodológica para contribuir
al desarrollo de la capacidad para resolver problemas matemáticos fortalece las
dimensiones del aprendizaje desarrollador: Motivación, activación-regulación,
significatividad con conceptos y aportes del enfoque cognitivista, histórico
social y dialectico, holístico holográfico. Está concebida para desarrollarse en
seis fases o momentos, subordinadas a las dimensiones: motivación,
activación-regulación, significatividad en el proceso de enseñanza –
aprendizaje de la resolución de problemas matemáticos y de manera indirecta se
desarrolla el pensamiento lógico matemático.
REFERENCIAS
Álvarez, E y Álvarez de Zayas, C. (2004) Elementos Epistemológicos
de la Matemática y su enseñanza. Bolivia: Kipus
Álvarez, C. (2014) Didactica Elemental. Bolivia: Kipus
Capote,
M. (2003) Una estructuración didáctica para la etapa de orientación en la
solución de problemas aritméticos con texto en el primer ciclo de la escuela
primaria. Tesis Doctorado en Ciencias Pedagógicas Universidad “Hermanos Saiz
Montes de Oca”, Pinar del Río
Castellanos,
D. (2001) Hacia una concepción del aprendizaje desarrollador. 1. ed. La Habana:
Instituto Superior Pedagógico “Enrique José Varona”
Condemarín,
M. (1989) Madurez Escolar. Ediciones UC. Santiago de Chile
Frege, G.
(1918) Los fundamentos de la aritmética. Madrid
Hegel, G. W. F. (1830) Enciclopedia
de las Ciencias Filosóficas. Traducción española de E. Ovejero y Maury
México: Editorial Porrúa, 1997
Henle, M. (1962): “Sobre la
relación entre la Lógica y el Pensamiento”. En: J. Delval (Compilador): Investigaciones
sobre lógica y psicología. Madrid: Alianza, 1977
Inhelder y Piaget
(1985) De la lógica del niño a la lógica del adolescente: Ensayo sobre la
construcción de las estructuras operatorias formales. (Cevasco, traductor).
Paidos Barcelona
Koliaguin,
Y. M. (1975) Metodología de la enseñanza de la Matemática en la escuela media.
1. ed. Moscú: Editorial Instrucción
Llivina,
M. (1999) ¿Modelos para resolver problemas? En Revista de Educación Matemática.
Departamento de Matemáticas. Universidad Tecnológica de Pereira. Colombia.
Número 3
Müller,
H. (1978) El trabajo heurístico y la ejercitación en la enseñanza de la
Matemática en la enseñanza general, politécnica y laboral. - Instituto Superior
Pedagógico “Frank País García”, Santiago de Cuba
Piaget,
J. (1969) La Construcción de lo real en el niño. Edición Revolucionaria, La
Habana, Cuba
Polya,
G. (1973) How solve it. A New Aspect of Mathematical Method. 2. ed.
New Jersey: Princeton University Press
Rodríguez, J. B. (2003) Una Propuesta Metodológica para la
utilización de las tecnologías de la información y las comunicaciones en el
proceso de
enseñanza-aprendizaje
de las funciones matemáticas. Tesis Doctorado Instituto Superior
Pedagógico “Enrique José Varona”, La Habana
Ron, J.
(2007) Una Estrategia Didáctica para el proceso de enseñanza-aprendizaje de la
Resolución de Problemas en las clases de Matemática en la educación Secundaria
Básica. Tesis Doctorado. Instituto Superior Pedagógico “Enrique José
Varona”, La Habana
Santos,
M. S. (1993) A metodologia de resolução de problemas como atividade de
investigação: um instrumento de mudança didática. Tese (Doutorado em Educaçao)
- Faculdade de Educação, Universidade de São Paulo, São Paulo
Schoenfeld,
A. H. (1992) Learning to think mathematically: problem solving, metacognition,
and sense-making in mathematics. En: GROUWS, D. (Ed.). The Handbook for
Research on Mathematics Teaching and Learning. New York: Mac Millan
Silvestre,
M. (2001) Aprendizaje, educación y desarrollo. 1. ed. La Habana: Editorial
Pueblo y Educación. Universität de Valencia
Spinoza, B. (1988). Tratado de la
reforma del entendimiento. s/e.
Vargas, W. (2020)
Metodología de la enseñanza aprendizaje de la matemática orientada al
desarrollo del pensamiento lógico matemático para estudiantes de Segundo de
secundaria. Tesis Doctoral. Universidad Autónoma del Beni
Horizontes. Revista de Investigación en Ciencias
de la Educación